Black holes
White dwarfs
Giants/Supergiants
Pulsars
Neutron stars
Halley's armada
Webb Space telescope
Hubble Space telescope
Mission to Mars
Extrasolar planets
Space race
Strategic defense initiative
Big Bang
Radio astronomy
Big Crunch?
Data from meteorites (shooting stars)
The Drake equation
Determining the ages of space objects
Moons of other planets - modern data
Asteroid expeditions
Time travel ???
General relativity
Special relativity (time dilation, length contraction)
String theory
Quantum Mechanics
Variable stars
Voyager
Mariner
Apollo
Mercury
Pioneer
Speed of light - how to measure
Space elevator?
Thursday, March 31, 2016
Spring Observing Lab
Lab 5 - Observing II: The Spring Sky
Despite the rain, the late winter
and early spring skies present some good opportunities for viewing. Heat haze is low, though precipitation can be
a problem for telescopes. In this lab,
you will locate several gems of the spring sky, drawing and identifying what
you see. So get out there and dig the
night sky!
Note: On sky maps, relative brightnesses are
indicated by the size of the dots. Also,
you may find it useful to use the reverse side of the chart to answer some of
the other questions. Also, skymaps.com
is a good resource to use.
1. If you look directly
overhead (to the zenith), what do you see?
2. What constellation(s) lie
directly overhead?
3. What asterism(s) are
visible?
4. What are the brightest objects
visible tonight? Name and locate them.
5. What are the stars of the
Summer Triangle? Can you see any of them
yet?
6. Find the Big Dipper. Can you see the double star in the handle? Can you see any other stars of Ursa Major?
7. Follow the arc of the handle
toward the next bright star. What star
is this?
8. Follow the pointer stars of
the Dipper to the next bright star (Polaris).
Draw the Dipper and Polaris as you see it. Can you see any other stars of Ursa Minor?
9. Is Polaris especially
bright? That is, is it one of the 5
brightest stars visible tonight?
10. Continuing on, following the
pointer stars past this star and curving a bit, find Cassiopeia. Draw what you see.
11. What is the lowest object
you can see on your horizon?
12. What planet(s) is/are
visible at this time?
13. Can you detect any color in
stars or planets? Comment.
14. What Messier (M) objects
should be visible (through a telescope) this evening?
15. List other interesting
events worth viewing this month.
16. How have the skies changed
since you first observed back in the winter?
17. Comment on the general
viewing conditions in your region.
Questions
1. What are the easiest ways to tell the
difference between a star and a planet?
2. When is the next full Moon?
Star Stuff 4 - Star Types
There are 4 fundamental forces of nature:
Strong nuclear - this keeps protons close together
Weak nuclear a responsible for radioactive decay
Electromagnetism - light, electricity, magnetism, etc
Gravity - weakest of all, but furthest reaching
A star (Latin root stella-) is essentially a ball of gas powered by nuclear reactions, held together by gravity.
Stars may appear white, but their color is a combination of many colors (and non visible e-m waves like UV).
Spectral types are listed in order of decreasing temperature:
O B A F G K M
with a temperature range from 60,000 K down to under 3500 K.
There are further subdivisions (C and S stars under M).
You can learn a lot about a star from where it lies on the Hertzsprung-Russel diagram.
The H-R diagram plots magnitude (brightness, from dim to bright) vs. temperature (high to low, usually as spectral type).
Hottest stars are on the left if the graph - they are normally brighter than cooler stars.
Most stars fall on along a diagonal band from upper left to lower right on the H-R diagram. We call this the Main Sequence, and the stars there are main sequence stars or dwarfs (which is a misleading term).
Stars above and to the right of the MS are giants (including supergiants).
Faint hit objects (white dwarfs) are below and to the left of the MS.
Our own Sun is a G2 star, somewhere close to 4.6 billion years old.
>
Strong nuclear - this keeps protons close together
Weak nuclear a responsible for radioactive decay
Electromagnetism - light, electricity, magnetism, etc
Gravity - weakest of all, but furthest reaching
A star (Latin root stella-) is essentially a ball of gas powered by nuclear reactions, held together by gravity.
Stars may appear white, but their color is a combination of many colors (and non visible e-m waves like UV).
Spectral types are listed in order of decreasing temperature:
O B A F G K M
with a temperature range from 60,000 K down to under 3500 K.
There are further subdivisions (C and S stars under M).
You can learn a lot about a star from where it lies on the Hertzsprung-Russel diagram.
The H-R diagram plots magnitude (brightness, from dim to bright) vs. temperature (high to low, usually as spectral type).
Hottest stars are on the left if the graph - they are normally brighter than cooler stars.
Most stars fall on along a diagonal band from upper left to lower right on the H-R diagram. We call this the Main Sequence, and the stars there are main sequence stars or dwarfs (which is a misleading term).
Stars above and to the right of the MS are giants (including supergiants).
Faint hit objects (white dwarfs) are below and to the left of the MS.
Our own Sun is a G2 star, somewhere close to 4.6 billion years old.
>
Friday, March 18, 2016
Good video
Brian Cox is a British astrophysicist who has produced some great BBC documentaries over the past few years. Here is episode 1 of his "Wonders of the Universe" series. Some of us watched part of it on Friday.
http://www.dailymotion.com/video/xyr1ly_wonders-of-the-universe-destiny_shortfilms
He also has a "Wonders of the Solar System" series and a "Wonders of Life" series. All good stuff.
http://www.dailymotion.com/video/xyr1ly_wonders-of-the-universe-destiny_shortfilms
He also has a "Wonders of the Solar System" series and a "Wonders of Life" series. All good stuff.
Star Stuff 3 - The Doppler Effect
You have no doubt heard about the Doppler Effect - what is it exactly? The key in the Doppler effect is that motion makes the "detected" or "perceived" frequencies higher or lower. We will consider this first for sound and then generalize to light.
Let's play around with this:
Let's play around with this:
http://www.lon-capa.org/~mmp/applist/doppler/d.htm
How how the number of waves you receive per second will be the same regardless of where you stand, UNLESS the source is moving. And then:
How how the number of waves you receive per second will be the same regardless of where you stand, UNLESS the source is moving. And then:
If the source is moving toward you, you detect/measure a higher frequency - this is called a BLUE SHIFT.
If the source is moving away from you, you detect/measure a lower frequency - this is called a RED SHIFT.
If the source is moving away from you, you detect/measure a lower frequency - this is called a RED SHIFT.
It's worth noting that the effect also works in reverse. If you (the detector) move toward a sound-emitter, you'll detect a higher frequency. If you (the detector) move away from a sound-emitter, you'll detect a lower frequency.
Mind you, these Doppler effects only happen WHILE there is relative motion between source and detector (you).
And they also work for light. In fact, the terms red shift and blue shift refer mainly to light (or other electromagnetic) phenomena.
If your computer runs Java:
If your computer runs Java:
http://falstad.com/mathphysics.html
Run the Ripple tank applet -
http://falstad.com/ripple/
Distant galaxies in the universe are moving away from us, as determined by their red shifts. This indicates that the universe is indeed expanding (first shown by E. Hubble). The 2011 Nobel Prize in Physics went to local physicist Adam Riess (and 2 others) for the discovery of the accelerating expansion of the universe. Awesome stuff!
http://www.nobelprize.org/nobel_prizes/physics/laureates/2011/
Star Stuff - 2, Electromagnetic Waves
Recall that waves can be categorized into two major divisions:
Mechanical waves, which require a medium. These include sound, water and waves on a (guitar, etc.) string
Electromagnetic waves, which travel best where there is NO medium (vacuum), though they can typically travel through a medium as well. All electromagnetic waves can be represented on a chart, usually going from low frequency (radio waves) to high frequency (gamma rays). This translates to: long wavelength to short wavelength.
All of these EM waves travel at the same speed in a vacuum: the speed of light (c). Thus, the standard wave velocity equation becomes:
where c is the speed of light (3 x 10^8 m/s), f is frequency (in Hz) and the Greek letter, lambda is wavelength (in m).
Mechanical waves, which require a medium. These include sound, water and waves on a (guitar, etc.) string
Electromagnetic waves, which travel best where there is NO medium (vacuum), though they can typically travel through a medium as well. All electromagnetic waves can be represented on a chart, usually going from low frequency (radio waves) to high frequency (gamma rays). This translates to: long wavelength to short wavelength.
All of these EM waves travel at the same speed in a vacuum: the speed of light (c). Thus, the standard wave velocity equation becomes:
where c is the speed of light (3 x 10^8 m/s), f is frequency (in Hz) and the Greek letter, lambda is wavelength (in m).
General breakdown of e/m waves from low frequency (and long wavelength) to high frequency (and short wavelength):
Radio
Microwave
IR (infrared)
Visible (ROYGBV)
UV (ultraviolet)
X-rays
Gamma rays
In detail, particularly the last image:
http://www.unihedron.com/projects/spectrum/downloads/full_spectrum.jpg
Don't forget - electromagnetic waves should be distinguished from mechanical waves (sound, water, earthquakes, strings on a guitar/piano/etc.).
Don't forget - electromagnetic waves should be distinguished from mechanical waves (sound, water, earthquakes, strings on a guitar/piano/etc.).
ALL E/M waves (in a vacuum) travel at the SPEED OF LIGHT (c).

Sunday, March 13, 2016
Thursday, March 10, 2016
Problems to play with - a homework assignment
I would like you to work on these questions next week - to be turned in by the end of the week. You can start to think about them early if you wish.
Radius of Earth = 6.4 x 10^6 m
Radius of Earth = 6.4 x 10^6 m
Radius of Moon = 1.74 x 10^6 m
Radius of Sun = 6.96 x 10^8 m
Distance from Earth to Sun (on average; one "Astronomical Unit" or AU) = 1.5 x 10^11 m
Distance from Earth to Moon = 3.84 x 10^8 m
Mass of Sun (one "solar mass") = 2 x 10^30 kg
Mass of Earth = 6 x 10^24 kg
Speed of light (in a vacuum) = c = 3 x 10^8 m/s
For constant (or average) speed: v = d/t
For constant (or average) speed: v = d/t
Calculate the following:
1. Distance between Earth and Moon, in Moon diameters.
2. Distance from Earth to Sun, in Earth diameters
3. Amount of time it takes light to reach the Earth from the Moon, in seconds.
4. Amount of time it takes light from the Sun to reach Earth, in minutes
5. Amount of time required for light to travel from the Sun to Pluto (40 AU from the Sun, on average) in hours
6. Ratio of Earth diameter to Moon diameter
7. How far light travels in one minute (LM)
8. Ratio of Sun diameter to Earth diameter
9. Distance to nearest star (other than Sun) - find the star and the distance (by looking it up)
10. Approximately how great a distance could light travel during your lifetime? (This could be termed a "light-lifespan", if you like.)
11. If you could travel at Earth's escape velocity (11,200 m/s), how long would it take you to reach the Moon? How long would it take you to reach the nearest star (see 9 above)?
12. Ratio of the biggest planet (Jupiter) diameter to Earth (diameter)
11. If you could travel at Earth's escape velocity (11,200 m/s), how long would it take you to reach the Moon? How long would it take you to reach the nearest star (see 9 above)?
12. Ratio of the biggest planet (Jupiter) diameter to Earth (diameter)
Friday, March 4, 2016
Formation of the Solar System
~ 4.6 billion years ago huge cloud of gas and dust started collapsing gravitationally
• As it collapsed it spun faster (conservation of angular momentum)
• No (or little) spin in the perpendicular plane
• Local clusters of dust and gas condensed - protosun formed first
• As material cooled, it condensed but never stopped rotating (rotates still since there’s nothing to stop it)
• Cores probably formed first, then attracted neighboring materials to form: planetesimal, protoplanet
• Probably not a unique system - there is increasing evidence for the existence of many other planetary systems
• Still an evolving theory
• All planets revolve around the sun in the same direction, but 3 have different directions of rotation (relative to the rest and to the direction of solar system motion) - Uranus, Venus, (Pluto)
The Terrestrial Planets: Mercury, Venus, Earth, and Mars
Relative Characteristics:
Planet Distance Period Radius Mass
Mercury 0.4 0.24 0.38 0.055
Venus 0.7 0.62 0.95 0.82
Earth 1 1 1 1
Mars 1.5 1.88 0.53 0.11
The Jovian Planets (gas giants)
Jupiter 5.2 11.9 11.2 318
Saturn 9.5 29.5 9.3 95
Uranus 19 84 4.0 14.6
Neptune 30 165 3.9 17.2
• As it collapsed it spun faster (conservation of angular momentum)
• No (or little) spin in the perpendicular plane
• Local clusters of dust and gas condensed - protosun formed first
• As material cooled, it condensed but never stopped rotating (rotates still since there’s nothing to stop it)
• Cores probably formed first, then attracted neighboring materials to form: planetesimal, protoplanet
• Probably not a unique system - there is increasing evidence for the existence of many other planetary systems
• Still an evolving theory
• All planets revolve around the sun in the same direction, but 3 have different directions of rotation (relative to the rest and to the direction of solar system motion) - Uranus, Venus, (Pluto)
The Terrestrial Planets: Mercury, Venus, Earth, and Mars
Relative Characteristics:
Planet Distance Period Radius Mass
Mercury 0.4 0.24 0.38 0.055
Venus 0.7 0.62 0.95 0.82
Earth 1 1 1 1
Mars 1.5 1.88 0.53 0.11
The Jovian Planets (gas giants)
Jupiter 5.2 11.9 11.2 318
Saturn 9.5 29.5 9.3 95
Uranus 19 84 4.0 14.6
Neptune 30 165 3.9 17.2
Wednesday, March 2, 2016
Planet "lab"
I decided against the idea of Planet presentation in favor of a "Planet Quest" lab. This will be due in 2 classes.
Lab 4 - Tour of the Planets
Please answer the following questions, based on your reading and web discovery. Some questions might have several answers, while the answer to others might be "none of them."
Which planet(s):
1. Rotates backwards?
2. Revolves backwards?
3. Rotates nearly on its side?
4. Have more than 10 moons?
5. Have only one moon?
6. Has an orbit with the greatest inclination to the ecliptic?
7. Is the furthest planet known to the ancients?
8. Has a largely methane atmosphere?
9. Has a nondescript, pale greenish color?
10. Has a blemish known as the great dark spot?
11. Has a fine iron oxide regolith?
12. Is most similar to Earth in its surface gravity?
13. Has the greatest mass?
14. Has the smallest diameter?
15. Have been visited by humans?
16. Has the strongest magnetic field?
17. Has rings?
18. Has sulfuric acid clouds?
19. Has the tallest mountain in the Solar System (and what is it)?
20. Has a day longer than its year?
21. Has been landed on most recently by spacecraft?
22. Experiences global dust storms?
23. Has a moon that rotates retrograde (and what is it)?
24. Was once thought to be a failed star?
25. Is heavily cratered?
26. Has moons which are likely candidates for life?
27. Was hit by a large comet in the last several years?
28. Is most oblate?
Now for the minor bodies.
1. Which body is an asteroid with its own orbiting asteroid?
2. Which moon has erupting volcanoes?
3. Which body is the largest asteroid?
4. Approximately how many known asteroids are there?
5. Approximately how many known Kuiper objects are there? What is the Kuiper belt?
6. How large is the Oort Cloud? What is the Oort Cloud?\
7. What are the Galilean satellites?
8. Which moon was the first discovered after the Galilean satellites?
9. What are Sedna and Eris?
10. What exactly is Pluto?
Etcetera – Write anything else of interest you have uncovered during this exercise.
Star stuff - 1
Big Distances
Consider light as a means of measurement. The speed of light (in a vacuum) is:
c = 3E8 m/s
(Which is around 186,000 miles per second or 670 million miles per hour, or nearly 7 times around the Earth's equator in one second.)
Since v = d/t, we see that d = v t.
Using light's speed, we can define a light-second:
1 LS = 3 E10 m
Similarly, a light year:
1 LY = 9.4607 E12 km (or nearly 6 trillion miles)
Angular Measurement
Consider light as a means of measurement. The speed of light (in a vacuum) is:
c = 3E8 m/s
(Which is around 186,000 miles per second or 670 million miles per hour, or nearly 7 times around the Earth's equator in one second.)
Since v = d/t, we see that d = v t.
Using light's speed, we can define a light-second:
1 LS = 3 E10 m
Similarly, a light year:
1 LY = 9.4607 E12 km (or nearly 6 trillion miles)
Angular Measurement
Consider the following convention which has been with us since the
rise of Babylonian mathematics:
There are 360 degrees per circle.
Each degree can be further divided into 60 minutes (60'), each called
an arcminute.
Each arcminute can be divided into 60 seconds (60"), each called an arcsecond.
Therefore, there are 3600 arcseconds in one degree.
Some rough approximations:
A fist extended at arm's length subtends an angle of approx. 10º.
A thumb extended at arm's length subtends an angle of approx. 2º.
The Moon (and Sun) subtend an angle of approx. 0.5º.
Human eye resolution (the ability to distinguish between 2 adjacent
objects) is limited to about 1 arcminute – roughly the diameter of a
dime at 60-m. Actually, given the size of our retina, we're limited
to a resolution of roughly 3'
So, to achieve better resolution, we need more aperture (ie., telescopes).
The Earth's atmosphere limits detail resolution to objects bigger than
0.5", the diameter of a dime at 7-km, or a human hair 2 football
fields away. This is usually reduced to 1" due to atmospheric
turbulence.
The parsec (pc)
definite as one parsec – that is, it has a parallax of one arcsec.
For example, if a star has a parallax angle (d) of 0.5 arcsec, it is
1/0.5 parsecs (or 2 parsecs) away.
The parsec (pc) is roughly 3.26 light years.
Distance (in pc) = 1 / d
where d is in seconds of arc.
Measuring star distances can be done by measuring their angle of
parallax – typically done over a 6-month period, seeing how the star's
position changes with respect to background stars in 6 months, during
which time the Earth has moved across its ellipse.
Unfortunately, this is limited to nearby stars, some 10,000. Consider
this: Proxima Centauri (nearest star) has a parallax angle of 0.75" –
a dime at 5-km. So, you need to repeat measurements over several
years for accuracy.
This works for stars up to about 300 LY away, less than 1% the
diameter of our galaxy!
[If the MW galaxy were reduced to 130 km (80 mi) in diameter, the
Solar System would be a mere 2 mm (0.08 inches) in width.]
Apparent magnitude (m) scale
bright or small.
Ptolemy classified things into numbers: 1-6, with 1 being brightest.
The brightest (1st magnitude) stars were 100 times brighter than the
faintest (6th magnitude). This convention remains standard to this
day. Still, this was very qualitative.
In the 19th century, with the advent of photographic means of
recording stars onto plates, a more sophisticated system was adopted.
It held to the original ideas of Ptolemy
A difference of 5 magnitudes (ie., from 1 to 6) is equivalent to a
factor of exactly 100 times. IN other words, 1st magnitude is 100x
brighter than 6th magnitude. Or, 6th magnitude is 1/100th as bright
as 1st mag.
This works well, except several bodies are brighter than (the
traditional) 1st mag.
So….. we have 0th magnitude and negative magnitudes for really bright objects.
Examples:
Sirius (brightest star): -1.5
Sun: -26.8
Moon: -12.6
Venus: -4.4
Canopus (2nd brightest star): -0.7
Faintest stars visible with eye: +6
Faintest stars visible from Earth: +24
Faintest stars visible from Hubble: +28
The magnitude factor is the 5th root of 100, which equals roughly
2.512 (about 2.5).
Keep in mind that this is APPARENT magnitude, which depends on
distance, actual star luminosity and interstellar matter.
Here's a problem: What is the brightness difference between two
objects of magnitudes -1 and 6?
Since they are 7 magnitudes apart, the distance is 2.5 to the 7th power, or 600.
For the math buffs: the formula for apparent magnitude comparison:
m1 – m2 = 2.5 log (I2 / I1)
The m's are magnitudes and the I's are intensities – the ratio of the
intensities gives a comparison factor. A reference point is m = 100,
corresponding to an intensity of 2.65 x 10^-6 lumens.
Absolute Magnitude, M
how we define absolute magnitude (M).
It depends on the star's luminosity, which is a measure of its brightness:
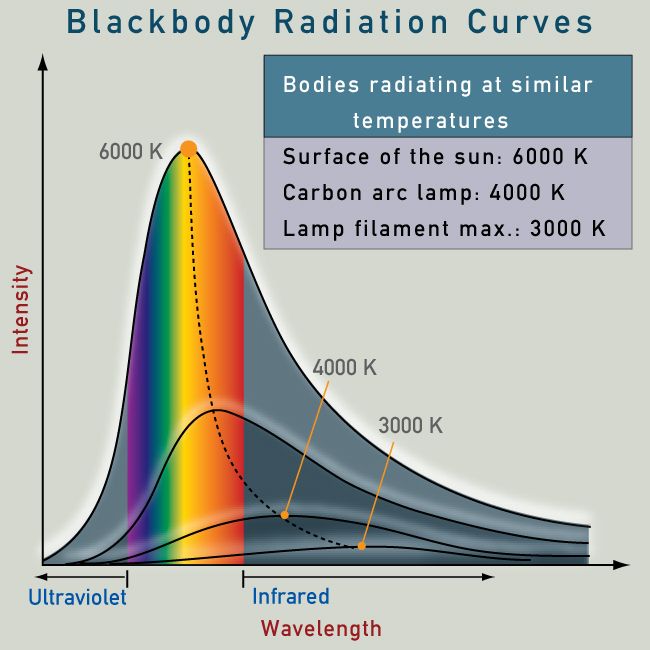
L = 4 pi R^2 s T^4
R is the radius of the body emitting light, s is the Stefan-Boltzmann
constant (5.67 x 10-8 W/m^2K^4) and T is the effective temperature (in
K) of the body.
constant (5.67 x 10-8 W/m^2K^4) and T is the effective temperature (in
K) of the body.
So, a star's luminosity depends on its size (radius, R) and absolute temperature (T).
If the star is 10 pm away, its M = m (by definition).
m – M = 5 log (d/10)
We let d = the distance (in pc), log is base 10, m is apparent
magnitude and M is absolute magnitude.
Subscribe to:
Comments (Atom)





